| |
|
|
| |
數學與程式 |
|
| |
|
|
| |
|
|
| |
邏輯思維 |
|
| |
|
|
| |
|
邏輯的起源 |
|
|
| |
|
|
|
|
|
|
| |
|
|
邏輯是個很抽象的名詞,這個詞彙最早源自於希臘,古希臘已經發展出訓練邏輯的方法,主要就是幾何原本,我們將古希臘的研究者稱為哲學家,因為在那時所有的科學都是哲學家們進行發展,包括了社會學、心理學、數學等等,在後續的發展中才逐漸演變出各式各樣的專門科學,所以我們一般也都將古希臘哲學稱為科學之母。 |
|
|
|
| |
|
|
|
|
|
|
| |
|
|
邏輯(英語:logic)的字根源起於希臘語邏各斯(希臘語:λόγος),最初的意思有詞語、思想、概念、推理、論點之意。後譯為(法語:logique),最後發展為英文中的邏輯(英語:logic)。 |
|
|
|
| |
|
|
|
|
|
|
| |
|
甚麼是邏輯 |
|
|
| |
|
|
以維基百科中的解釋,邏輯被說明如下: |
|
|
|
| |
|
|
|
|
|
|
| |
|
|
邏輯(古希臘語:λογική;德語:Logik;法語:logique;英語:logic;義大利語、西班牙語、葡萄牙語: logica),又稱理則、論理、推理、推論,是對有效推論的哲學研究[1]。邏輯被使用在大部份的智能活動中,但主要在心理、學習、哲學、語義學、數學、推論統計學、腦科學、法律和電腦科學等領域內被視為一門學科。邏輯討論邏輯論證會呈現的一般形式,哪種形式是有效的,以及其中的謬論。 |
|
|
|
| |
|
|
邏輯通常可分為三個部份:歸納推理、溯因推理和演繹推理。 |
|
|
|
| |
|
|
在哲學裡,邏輯被應用在大多數的主要領域之中:形上學/宇宙論、本體論、知識論及倫理學。 |
|
|
|
| |
|
|
在數學裡,邏輯是指形式邏輯和數理邏輯,形式邏輯是研究某個形式語言的有效推論[2]。主要是演繹推理。 在辯證法中也會學習到邏輯[3]。數理邏輯是研究抽象邏輯關係和數學基本的問題。 |
|
|
|
| |
|
|
在心理、腦科學、語義學、法律裡,是研究人類思想推理的處理。 |
|
|
|
| |
|
|
在學習、推論統計學裡,是研究最大可能的結論。主要是歸納推理、溯因推理。 |
|
|
|
| |
|
|
在電腦科學裡, 是研究各種方法的性質,可能性,和實現在機器上。主要是歸納推理、溯因推理,也有在歸納推理的研究。 |
|
|
|
| |
|
|
從古文明開始(如古印度[註 1]、古中國[註 2]和古希臘)都有對邏輯進行研究。在西方,亞里斯多德將邏輯建立成一門正式的學科,並在哲學中給予它一個基本的位置。 |
|
|
|
| |
|
|
|
|
|
|
| |
|
邏輯的簡單解釋 |
|
|
| |
|
|
到了這裡,邏輯這個詞彙仍然是充滿抽象的,我們可以試圖以更簡單的概念來說明,邏輯是甚麼: |
|
|
|
| |
|
|
|
|
|
|
| |
|
|
邏輯是一步一腳印的思考。 |
|
|
|
| |
|
|
邏輯是一個蘿蔔一個坑的思考。 |
|
|
|
| |
|
|
邏輯是因為……所以……的思考。 |
|
|
|
| |
|
|
|
|
|
|
| |
|
|
在邏輯的思考中,都一定有一個確定的理由,才會產生後續的結果,也就是我們一般所說的科學精神,在科學中所有的學科都講究這樣的邏輯概念,我們才能得到不變的真理,數學也自然必須符合這樣的邏輯精神。 |
|
|
|
| |
|
|
|
|
|
|
| |
|
數學的思考邏輯 |
|
|
| |
|
|
|
|
|
|
| |
|
|
我們將幾何學稱為數學之母,因為最早的數學是由幾何發展而來的,在幾何學中已經發展出了邏輯性的思考與驗證的方法,也經常被用來訓練邏輯思考。 |
|
|
|
| |
|
|
下面是幾何學中的畢氏定理(勾股定理)證明,畢氏定理目前有超過400種的證明方法,我們列舉了古希臘哲學家歐幾里得在幾何原本一書中證明的方法: |
|
|
|
| |
|
|
|
|
|
|
| |
|
|
 |
|
|
|
| |
|
|
|
|
|
|
| |
|
|

|
|
|
|
| |
|
|
在這個證明中,我們可以看到每一個步驟,都是因為….所以….的論述方式,也就是一步一腳印地證明,完全以邏輯的思考方式來進行。 |
|
|
|
| |
|
|
|
|
|
|
| |
|
程式的思考邏輯 |
|
|
| |
|
|
我們以氣泡排序法(Bubble Sorting)來說明程式中邏輯思考的例子。 |
|
|
|
| |
|
|
|
|
|
|
| |
|
|
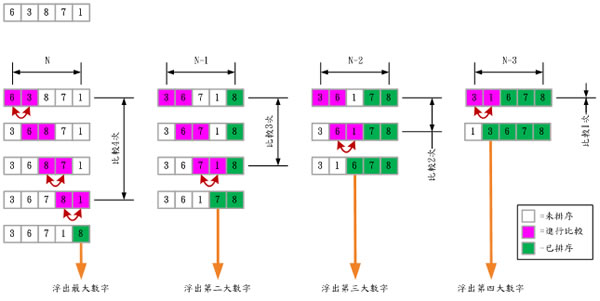
氣泡排序法是逐步地將相臨的資料互相比較,若發現前面的資料比後面的資料大時,就將資料互換。依次由左至右,會像氣泡般依次將最小的數字後往前浮起,最後所有的資料將會依照由小至大的順序排列。 |
|
|
|
| |
|
|
在這個例子中,我們需要整理出氣泡排序法的原則性,然後依照原則性推敲程式進行的各個步驟,也需要考慮在這樣的步驟中是否會發生錯誤的狀況,讓程式執行能夠完全正確,不會有錯誤發生。 |
|
|
|
| |
|
|
|
|
|
|
| |
|
氣泡排序法的思考步驟: |
|
|
| |
|
|
|
|
|
|
| |
|
|
 |
|
|
|
| |
|
|
|
|
|
|
| |
|
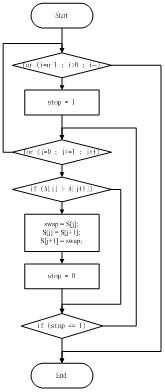
氣泡排序法的流程圖 |
|
|
| |
|
|
撰寫程式時,我們會利用流程圖的方式來幫助我們整理思考,讓邏輯清晰而正確。 |
|
|
|
| |
|
|
|
|
|
|
| |
|
|
下面的例子中,我們利用流程圖來一步一步地思考程式執行的步驟,並且容易看出可能的錯誤狀況。 |
|
|
|
| |
|
|
|
|
|
|
| |
|
|
|
|
|
|
| |
|
|
|
|
|
|
| |
|
氣泡排序法的程式碼 |
|
|
| |
|
|
|
|
|
|
| |
|
|
 |
|
|
|
| |
|
|
|
|
|
|
| |
簡化運算、提升效率 |
|
| |
|
|
|
|
|
|
| |
|
數列與級數 |
|
|
| |
|
|
|
|
|
|
| |
|
|
我們經常使用的例子為加總,將若干項的數字累加計算出總和。 |
|
|
|
| |
|
|
|
|
|
|
| |
|
|
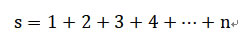 |
|
|
|
| |
|
|
|
|
|
|
| |
|
|
在級數中,我們必須對每一項的數字累加計算,所以我們需要計算n次,才能得到結果。 |
|
|
|
| |
|
|
|
|
|
|
| |
|
|
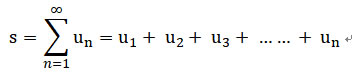 |
|
|
|
| |
|
|
|
|
|
|
| |
|
|
上面的級數經由數學的整理後,能夠得到一個加總的公式,在加總公式中,我們只需要進行3次的計算就能夠得到加總的結果。 |
|
|
|
| |
|
|
|
|
|
|
| |
|
|
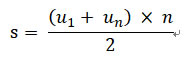 |
|
|
|
| |
|
|
|
|
|
|
| |
|
|
利用此類的數學公式,我們能夠以很少的計算次數,得到我們需要的結果。 |
|
|
|
| |
|
|
|
|
|
|
| |
|
簡化的方程式 |
|
|
| |
|
|
|
|
|
|
| |
|
|
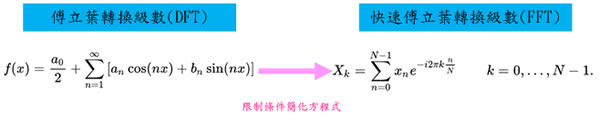
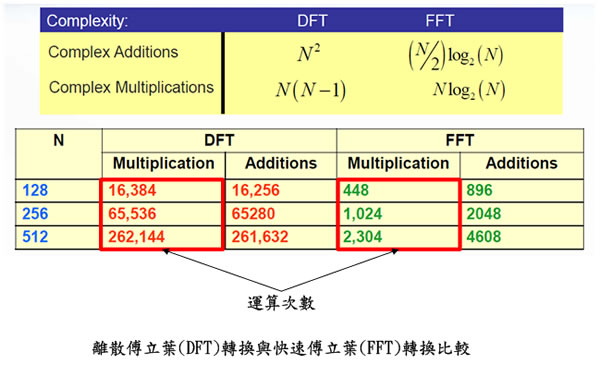
典型的例子是傅立葉轉換(Fourier Transform),數學上發展出很多種傅立葉轉換的計算方式,如離散傅立葉轉換(Discrete Fourier Transform,簡稱DFT)以及快速傅立葉轉換(Fast Fourier Transform,簡稱FFT),這兩者需要的計算次數就差異很大,如下表示一個以硬體執行計算的例子,標示出DFT與FFT的計算次數,在執行512個輸入樣本數的情形下,DFT需要262144次的執行次數,FFT則只需要2304次。這表示使用FFT計算時只需要使用DFT時的1/113的時間 |
|
|
|
| |
|
|
|
|
|
|
| |
|
|
 |
|
|
|
| |
|
|
|
|
|
|
| |
|
|
 |
|
|
|
| |
|
|
|
|
|
|
| |
實用的數學方法 |
|
| |
|
|
|
|
|
|
| |
|
|
程式中為了某些特定的目的,會直接使用數學的模型來達成目的,例如我們需要計算加總,我們就會直接利用級數的加總公式,我們想要計算平均數,就會利用統計的各種計算平均值的公式,在撰寫程式的時候,我們可以利用各式各樣的數學公式,就能夠較為專注在程式的其他判斷或式處理上,讓撰寫程式變得更有效率。 |
|
|
|
| |
|
|
|
|
|
|
| |
|
常見使用於程式中的數學 |
|
|
| |
|
|
|
|
|
|
| |
|
|
以下列舉了一些較為常見使用在程式中的的數學領域,也是一般會在高中大學時學習到的數學,如果能夠對這些數學有更多了解,能夠大幅增加程式撰寫的功力。 |
|
|
|
| |
|
|
|
|
|
|
| |
|
|
|
1.多元多次方程式 |
|
|
|
| |
|
|
|
2.三角函數 |
|
|
|
| |
|
|
|
3.級數 |
|
|
|
| |
|
|
|
4.微積分 |
|
|
|
| |
|
|
|
5.線性代數 |
|
|
|
| |
|
|
|
6.離散數學 |
|
|
|
| |
|
|
|
7.機率 |
|
|
|
| |
|
|
|
8.統計 |
|
|
|
| |
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
| |
|
|
|
|
|
|
| |
|
|
|
|
|
|
| |
|
|
| |
|
|
| |
|
|
| |
|
|
| |
|
|
| |
|
|
| |
|
|
| |
|
|
| |
|
|